Phase-field models have been used extensively in studying microstructure evolution in alloys and have the superiority of comprehending, predicting, and optimizing microstructure-sensitive macroscopic material properties. The elastic strain energy is a vital factor in modeling crystal structure formation in solid-solid phase transformations. Conventionally, it is computed in the reciprocal space according to the famous Khachaturyan-Shatalov theory. In large-scale simulations, the full-space Fourier transform becomes extremely time-consuming.

Recently, researchers from the High-Performance Department of our Center derive a formula for a real-space convolution kernel equivalent to the elastic energy density function that the Khachaturyan-Shatalov theory has in the reciprocal space. In addition, we provide an error upper bound estimation for kernel truncation, guided by which one can use a compact convolution kernel and still achieve the required accuracy. Based on the Center's autonomous and controllable "ORISE" supercomputing resources, this work achieves real-world βàωand βàαphase transformations in Ti-alloy. The code scales up to 4,096 accelerators, reaching 99.07% parallel efficiency.

This research result was accepted by the International Conference on Parallel Processing (ICPP) (CCF B) and reported. The first author of the paper is Gao Yaqian, a PhD student, supervised by researcher Chi Xuebin, and the corresponding author is researcher Zhang Jian. This work is supported by the National Key Research and Development Program of China under grant no. 2021YFB0300203.

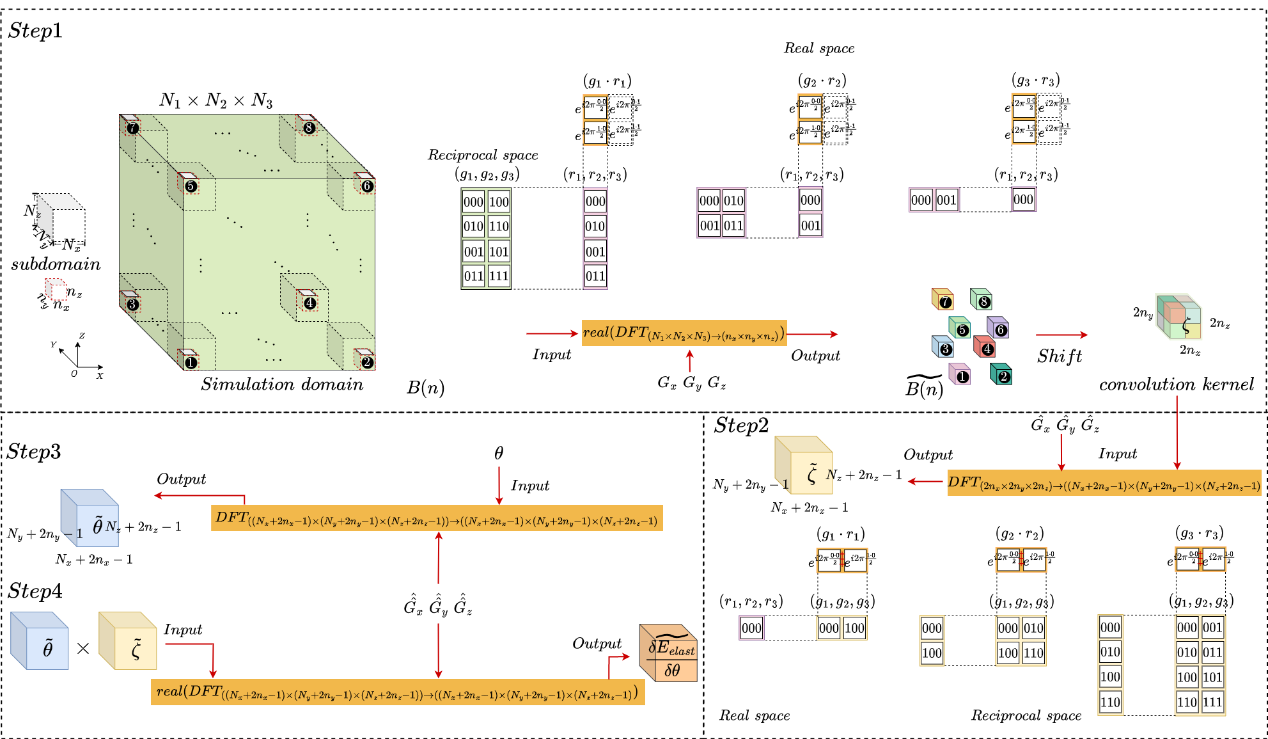
Fig. Steps of computing the elastic energy term using DFT-based convolution. 

Related Achievement：

Gao Y, Zhang J, Ye H, et al. Large-scale Phase-Field Simulations for Solid-Solid Phase Transformations involving Elastic Energy[C]//Proceedings of the 53rd International Conference on Parallel Processing. 2024: 377-387. https://doi.org/10.1145/3673038.3673066